Volumes of Other Cross-Sections
(Click on images to enlarge them)

Sample:  The base of a certain solid is the circle x²+y²=a².  Each plane section of the solid cut out by a plane perpendicular to the x-axis is a square with one edge of the square in the base of the solid.  Find its volume.

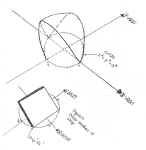
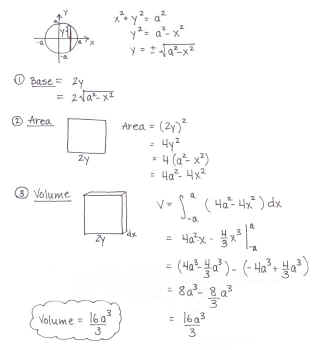
Build the volume of the cross-section one dimension at a time.  Sketch the base and write an expression for "the strip" which lies in the base.  Then determine the area for the specified shape of the cross-section.  Then put in the third dimension of thickness (dx or dy) and integrate to sum up            
all the "slices" for the entire solid.

Extra Practice Examples

1. Find the volume of the solid having as a base the circle x²+y²=4 and cross-sections perpendicular to the x-axis which are squares.
         Click here to check your work.

2. Find the volume of the solid having as a base the region enclosed by y=x+1 
   and y=x²-1 and cross-sections perpendicular to the x-axis which are rectangles of height 2.
         Click here to check your work.

3. Find the volume of the solid whose base is the area bounded by the lines
   y=1-(x/2),  y=-1+(x/2), and x=0, and whose cross-sections perpendicular to 
   the x-axis are equilateral triangles.
         Click here to check your work.